三角形中线公式推导(初中几何补充内容:中线长定理)
2024-11-03 09:06:40
一、什么是中线长定理?
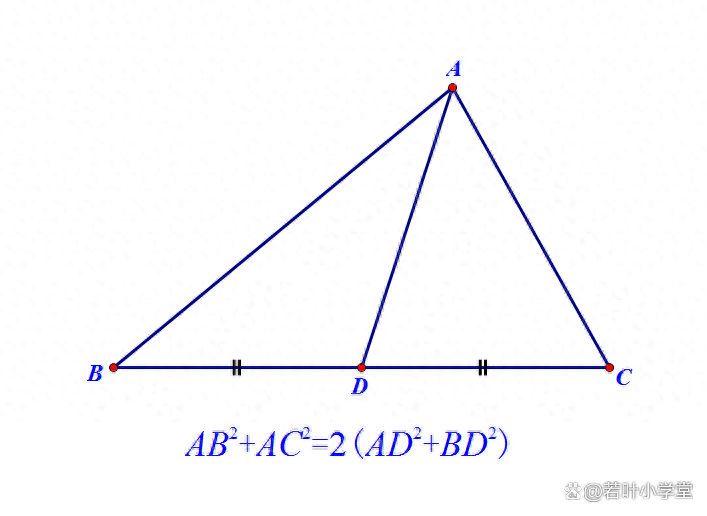
如图,AD是△ABC中BC边上的中线,则
AB^2+AC^2=2(AD^2+BD^2)=2(AD^2+CD^2)
二、中线长定理的证明
分析:看到平方,容易想到勾股定理,要用勾股定理,则需构造直角三角形,故想到过点A作BC边上的高,构造直角三角形后,运用勾股定理求解。
证明:过点A作AE⊥BC于点E
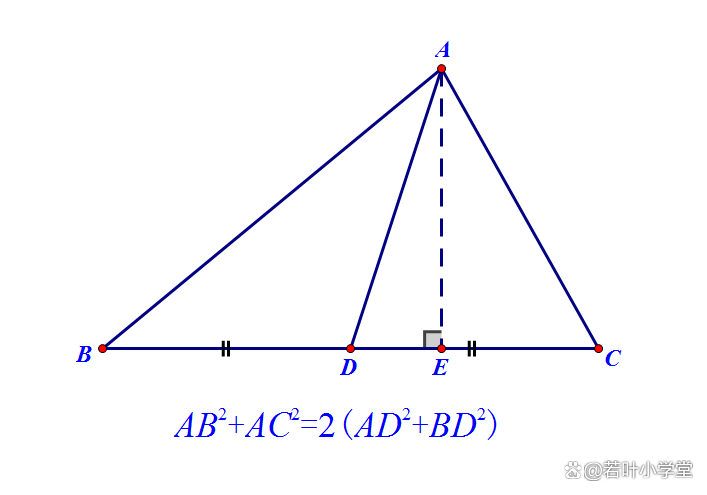
∵AD是△ABC中BC边上的中线
∴BD=CD
在RT△ADE中,由勾股定理,得
AE^2+DE^2=AD^2
在RT△ABE中,由勾股定理,得
AB^2=AE^2+(BD+DE)^2
=AE^2+BD^2+DE^2+2BD·DE
=AD^2+BD^2+2BD·DE
在RT△ACE中,由勾股定理,得
AC^2=AE^2+(CD-DE)^2
=AE^2+CD^2+DE^2-2BD·DE
=AD^2+BD^2-2BD·DE
∴AB^2+AC^2=2(AD^2+BD^2)=2(AD^2+CD^2)
三、小结
1、中线长定理提供了一种快速求中线长的方法,在某些填空压轴题中可以快速得到答案;
2、中线长定理可由勾股定理证明,构造直角三角形最常用的方法就是作高;
3、定理结论不建议死记硬背,多推导几遍就可以烂熟于胸。
