三角形中点的性质是什么（初中几何关于中点四大模型全解析）

秉着‬尽可能‬不‬重复‬不遗漏‬的原则‬，我把‬中点‬类‬归结‬为‬四大‬模型‬，如下‬：

►模型一：倍长中线或倍长类中线

►模型二： 等腰三角形底边中点

►模型三：中位线定理

►模型四：直角三角形斜边中线

模型解读

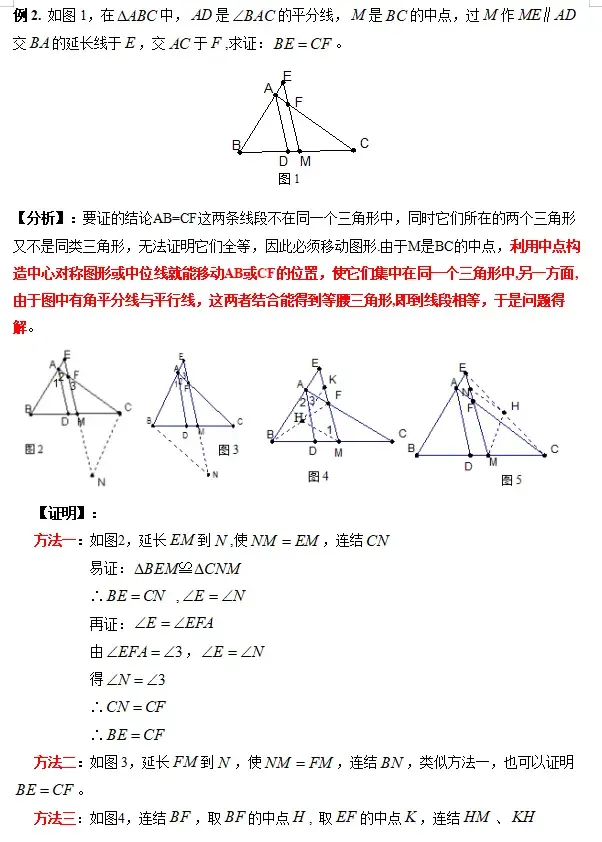
一、倍长中线或倍长类中线

可‬分为延长一倍的中线和延长k倍长的中线

（注：类中线的“类”可以理解为类似，不是真正意思上的中线，但可以类比成中线）

底层逻辑：当遇见中线或者中点的时候，可以尝试倍长中线或类中线，通过延长，构造全等三角形或平行四边形，目的是对已知条件中的线段进行转移。

如图①，AD 是△ABC 的中线，延长 AD 至点 E 使 DE＝AD，易证：△ADC≌△EDB（SAS）

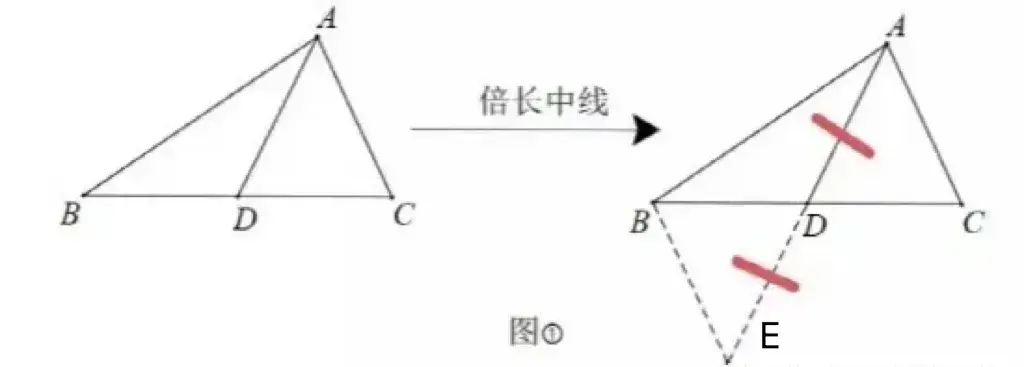
如图②，D 是 BC 中点，延长 FD 至点 E 使 DE＝FD，易证：△FDB≌△EDC（SAS）

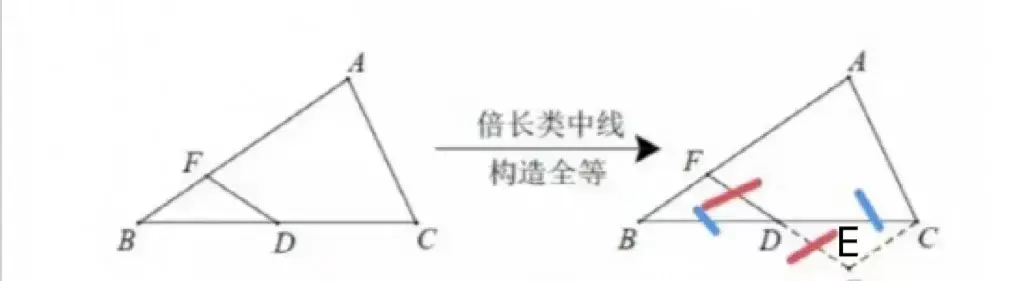
（1）延长1倍的中线：

如图，线段AD是三角形ABC的中线，延长线段AD至E，使DE=AD（即延长1倍的中线），再连接BE、CE。

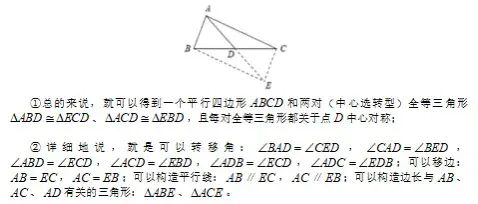
（2）延长k倍的中线：（k大于零且k不等于1）

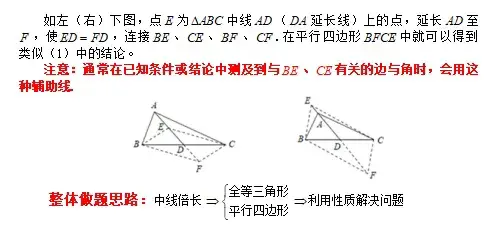
二、等腰三角形底边中点：

1.通常在以下两种情况下，会作“三线合一”辅助线：

① 等腰三角形中有底边中点；

② 证明底边中点。（证明角平分线和垂直也会用到）

2.作“三线合一”辅助线能得到：

① 整体上，“三线合一”作底边的垂直平分线出现对称模型；

② 角方面：可以出现等角和直角；线段方面：可以得到相等的线段。

三、中位线定理

1.中位线：连接三角形两边的中点所得的线段叫做三角形的中位线；也可以过三角形一边的中点作平行于三角形另外一边交于第三边所得的线段也是中位线；

以上是中位线的两种作法，第一种可以直接用中位线的性质，第二种需要说明理由为什么是中位线，再用中位线的性质.

2.中位线的性质：三角形的中位线平行于三角形的第三边，且等于第三边的一半；

3.中位线辅助线能起到的作用：

① 在线段大小关系上，三角形的中位线是三角形第三边的一半，起着传递线段长度的功能.

② 在位置上，三角形的中位线平行三角形的第三边，起着角的位置转移和计算角的的功能.

4.通常在以下两种情况下，会作中位线辅助线：

① 有两个（或两个以上）的中点时；

② 有一边中点，并且已知或求证中涉及到线段的倍分关系时。

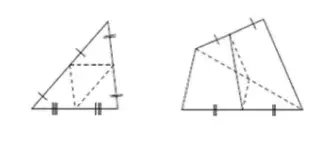
注意‬‼️‬熟悉以下两个图形（常考‬）

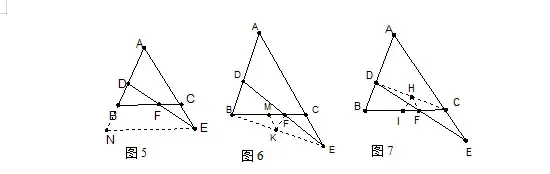
来看两道典型例题

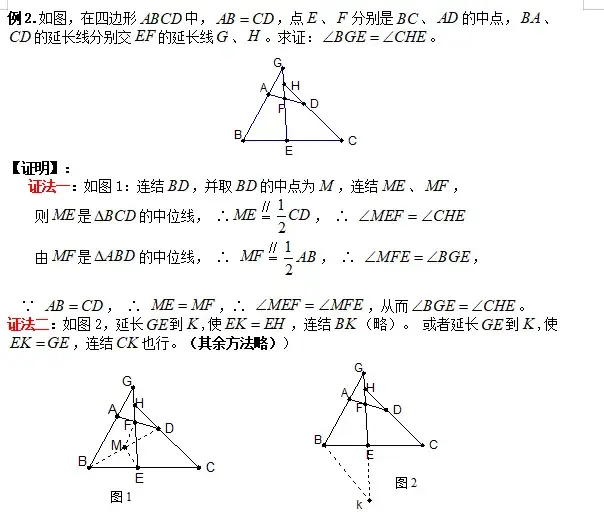
四、直角三角形斜边中线：

常见类型如下

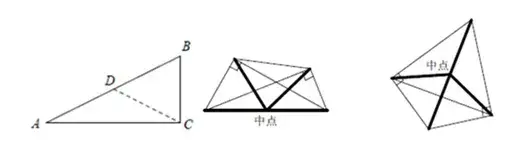
来看到典型例题

方法总结：

1.直角三角形，且出现了斜边的中线。

2.发现线段为斜边上的中线，且等于斜边的一半。

3.作斜边中线，可以构造出等腰三角形，从而得到相等的边、相等的角。

4.通常在知道直角三角形斜边的中点的情况下，想到作斜边中线这条辅助线。

以上为四种模型的解析，希望对你有帮助。